Die Rätsel des CT 2006 enthüllt
Der Kubus
 Ausgangspunkt des diesjährigen CT-Rätsels war ein riesiger Kubus, der mitten im Frühstückssaal aufgestellt worden war, und der von allen Seiten vor neugierigen Blicken in sein Innenleben geschützt war. Der einzige Zugang ins Innere, eine teilweise wegklappbare Seitenwand, war durch ein Zahlenschloss versperrt. Auf dieser Seitenwand (Bild siehe weiter unten) waren die römischen Ziffern von eins bis vier dargestellt; ebenso viele Zeilen, wie das Zahlenschloss Stellen hatte. Daneben befanden sich einige zunächst unverständliche Zeichnungen, für deren Entschlüsselung weitere wichtige Informationen fehlten. Es stellte sich heraus, dass sich diese Informationen verstreut in den Wäldern von Bernshausen befanden. Im Frühstückssaal ließ sich eine Karte ausmachen, deren blaue Markierungen die Standorte der weiteren Hinweise verraten sollten. [Ich habe jeweils den Ausgangspunkt oben rechts und den Treffpunkt links mit einem roten Punkt nachmarkiert.]
Ausgangspunkt des diesjährigen CT-Rätsels war ein riesiger Kubus, der mitten im Frühstückssaal aufgestellt worden war, und der von allen Seiten vor neugierigen Blicken in sein Innenleben geschützt war. Der einzige Zugang ins Innere, eine teilweise wegklappbare Seitenwand, war durch ein Zahlenschloss versperrt. Auf dieser Seitenwand (Bild siehe weiter unten) waren die römischen Ziffern von eins bis vier dargestellt; ebenso viele Zeilen, wie das Zahlenschloss Stellen hatte. Daneben befanden sich einige zunächst unverständliche Zeichnungen, für deren Entschlüsselung weitere wichtige Informationen fehlten. Es stellte sich heraus, dass sich diese Informationen verstreut in den Wäldern von Bernshausen befanden. Im Frühstückssaal ließ sich eine Karte ausmachen, deren blaue Markierungen die Standorte der weiteren Hinweise verraten sollten. [Ich habe jeweils den Ausgangspunkt oben rechts und den Treffpunkt links mit einem roten Punkt nachmarkiert.]
Die Forschergruppe teilte sich in Gruppen auf, um die Hinweise möglichst schnell einsammeln zu können. Nachdem alle Hinweise eingesammelt waren, konnte sich die Forschergruppe an deren Entschlüsselung begeben.
Die vier Zahlenrätsel
 Alle Teilrätsel aus den Wäldern mussten irgendwelche Zahlen hervorbringen, die mit Hilfe der Symbole auf der Öffnungsseite des Kubus zu den Ziffern für das Zahlenschloss umgewandelt werden könnten.
Alle Teilrätsel aus den Wäldern mussten irgendwelche Zahlen hervorbringen, die mit Hilfe der Symbole auf der Öffnungsseite des Kubus zu den Ziffern für das Zahlenschloss umgewandelt werden könnten.
Das Würfelrätsel
 In den Wäldern fanden sich insgesamt sieben farbige Schaumstoff-Bruchstücke, die sich richtig angeordnet zu einem Würfel zusammensetzen ließen. Da hierbei mehrere Lösungen möglich waren, war es wichtig, dass sich die beschrifteten Seiten der Bruchstücke nach Zusammensetzen des Würfels außen befanden. Richtig zusammengesetzt enthielt jede Seite des Würfels mittig eine Zahl umgeben von einem Kranz aus verschieden orientierten Linien.
In den Wäldern fanden sich insgesamt sieben farbige Schaumstoff-Bruchstücke, die sich richtig angeordnet zu einem Würfel zusammensetzen ließen. Da hierbei mehrere Lösungen möglich waren, war es wichtig, dass sich die beschrifteten Seiten der Bruchstücke nach Zusammensetzen des Würfels außen befanden. Richtig zusammengesetzt enthielt jede Seite des Würfels mittig eine Zahl umgeben von einem Kranz aus verschieden orientierten Linien.
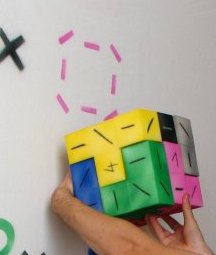 Diese Linienkränze passten jeweils auf die auf der Kubusseite dargestellten Linienkränze. Außerdem befand sich die zugehörige Ziffer des Würfels ebenfalls auf einem Schaumstoff-Bruchstück in der auf der Kubusseite dargestellten Farbe. Die Symbole konnten somit durch die zugehörigen Ziffern des Würfels ersetzt werden und die Gleichung las sich dann wie folgt:
<m>8-4*1=4</m>
Diese Linienkränze passten jeweils auf die auf der Kubusseite dargestellten Linienkränze. Außerdem befand sich die zugehörige Ziffer des Würfels ebenfalls auf einem Schaumstoff-Bruchstück in der auf der Kubusseite dargestellten Farbe. Die Symbole konnten somit durch die zugehörigen Ziffern des Würfels ersetzt werden und die Gleichung las sich dann wie folgt:
<m>8-4*1=4</m>
Das Farbrätsel
 In den Wäldern fanden sich weiterhin zwei Schatztruhen, die jeweils drei Fläschchen mit gefärbtem Wasser enthielten, Farbtinkturen in den Grundfarben gelb, rot und blau, Fläschchen mit klarem Wasser und der Hinweis, dass drei Tropfen der Farbtinkturen jeweils einer Einheit entsprächen. Ziel dieses Rätsels war es die Farben der Referenzfläschchen aus den Schatztruhen mit Hilfe der Farbtinkturen in den Grundfarben nachzubilden und die jeweils benötigten Tropfenmengen resp. die zugehörigen Einheiten zu notieren.
In den Wäldern fanden sich weiterhin zwei Schatztruhen, die jeweils drei Fläschchen mit gefärbtem Wasser enthielten, Farbtinkturen in den Grundfarben gelb, rot und blau, Fläschchen mit klarem Wasser und der Hinweis, dass drei Tropfen der Farbtinkturen jeweils einer Einheit entsprächen. Ziel dieses Rätsels war es die Farben der Referenzfläschchen aus den Schatztruhen mit Hilfe der Farbtinkturen in den Grundfarben nachzubilden und die jeweils benötigten Tropfenmengen resp. die zugehörigen Einheiten zu notieren.


Das Nagelbretträtsel
 Das Nagelbretträtsel und das Spinnennetzrätsel gehören rätseltechnisch zusammen, bilden aber sehr unterschiedliche Rätsel, weshalb ich sie hier gesondert erläutere. Für das Nagelbretträtsel fand sich den Wäldern eine mit 63 Nägeln bestückte Sperrholzplatte, deren Spalten mit den Ziffern 0 bis 9 und deren Zeilen mit den Buchstaben A bis ? beschriftet waren. Außerdem war dem Nagelbrett eine Rolle mit einer dünnen Schnur beigelegt. Der Verdacht lag also nahe, dass mit der Schnur durch Abstecken der richtigen Nägel eine Figur zu bilden war.
Das Nagelbretträtsel und das Spinnennetzrätsel gehören rätseltechnisch zusammen, bilden aber sehr unterschiedliche Rätsel, weshalb ich sie hier gesondert erläutere. Für das Nagelbretträtsel fand sich den Wäldern eine mit 63 Nägeln bestückte Sperrholzplatte, deren Spalten mit den Ziffern 0 bis 9 und deren Zeilen mit den Buchstaben A bis ? beschriftet waren. Außerdem war dem Nagelbrett eine Rolle mit einer dünnen Schnur beigelegt. Der Verdacht lag also nahe, dass mit der Schnur durch Abstecken der richtigen Nägel eine Figur zu bilden war.
 Die Hinweise dazu fanden sich ebenfalls im Wald. An diversen Bäumen waren die Teilstücke von insgesamt 24 beschrifteten und bebilderten Seiten aufgehangen, die zunächst zusammengesetzt werden mussten. Daraufhin ergaben sich auf jeder Seite jeweils zwei Bilder und jeweils eine zugehörige „Leseanleitung“ dafür. An der links abgebildeten Seite sei das Prinzip erklärt: Das erste Bild zeigt ein BUCH. Die darüber angebrachte Zahl 3 bedeutet, dass von diesem Wort der 3. Buchstabe auszuwählen ist, also das C. Darunter ist ein TURM abgebildet. Die Anweisung M-1 bedeutet hier: Nehme die Position des Buchstaben M (hier 4) und ziehe 1 davon ab, also 3. Somit ergibt sich insgesamt die Koordinate C3. Wenn man dieses Prinzip auch auf die anderen 23 Seiten anwandte, ergaben sich somit 24 Koordinaten des Nagelbrettes. Die korrekte Reihenfolge der Koordinaten wurde durch ein Zahlzeichen an den Ecken der Seiten angezeigt (siehe Anhang über das Zahlensystem). Die Koordinaten in der richtigen Reihenfolge auf dem Nagelbrett abgesteckt, ergaben dann die Figur der Zahl 12. Dies war die erste Zahl für die Rechnung der dritten Zeile.
Die Hinweise dazu fanden sich ebenfalls im Wald. An diversen Bäumen waren die Teilstücke von insgesamt 24 beschrifteten und bebilderten Seiten aufgehangen, die zunächst zusammengesetzt werden mussten. Daraufhin ergaben sich auf jeder Seite jeweils zwei Bilder und jeweils eine zugehörige „Leseanleitung“ dafür. An der links abgebildeten Seite sei das Prinzip erklärt: Das erste Bild zeigt ein BUCH. Die darüber angebrachte Zahl 3 bedeutet, dass von diesem Wort der 3. Buchstabe auszuwählen ist, also das C. Darunter ist ein TURM abgebildet. Die Anweisung M-1 bedeutet hier: Nehme die Position des Buchstaben M (hier 4) und ziehe 1 davon ab, also 3. Somit ergibt sich insgesamt die Koordinate C3. Wenn man dieses Prinzip auch auf die anderen 23 Seiten anwandte, ergaben sich somit 24 Koordinaten des Nagelbrettes. Die korrekte Reihenfolge der Koordinaten wurde durch ein Zahlzeichen an den Ecken der Seiten angezeigt (siehe Anhang über das Zahlensystem). Die Koordinaten in der richtigen Reihenfolge auf dem Nagelbrett abgesteckt, ergaben dann die Figur der Zahl 12. Dies war die erste Zahl für die Rechnung der dritten Zeile.
Das Spinnennetzrätsel
 Unmittelbar in der Nähe des Treffpunktes fand sich ein spinnennetzartiges Gebilde aus 12 Holzkästen, von denen die mittleren vier bereits mit jeweils vier Schaumstoffwürfeln gefüllt waren, und die mittels teilweise farbiger Schnüre verbunden waren.
Unmittelbar in der Nähe des Treffpunktes fand sich ein spinnennetzartiges Gebilde aus 12 Holzkästen, von denen die mittleren vier bereits mit jeweils vier Schaumstoffwürfeln gefüllt waren, und die mittels teilweise farbiger Schnüre verbunden waren.
dass in ganz Deutschland kein schwarzes Paketband aufzutreiben war, weshalb man kurzerhand silbernes Paketband mit Edding schwarz anmalte?
Aus den Wäldern hatten wir bereits entsprechend viele weitere Schaumstoffwürfel mitgebracht, um die Kästen komplett zu füllen. Sowohl auf den Kästen, als auch auf den Schaumstoffwürfeln war dazu eine Nummmer zwischen 1 und 8 aufmalt. Die Vorderseiten der Schaumstoffwürfel waren jeweils mit einem farbigen Buchstaben versehen, entsprechend der Farben der farbigen Verbindungsschnüre.
dass ursprünglich die Schaumstoffwürfel selbst die Farbe der Verbindungsschnüre erhalten sollten? Die verwendete Färbemethode brachte allerdings nur undefinierbare Pastelfarbtöne hervor, weshalb mit farbigen Buchstaben improvisiert wurde.
Wenn man nun den farbigen Verbindungsschnüren folgte und jeweils einen Buchstaben in der Farbe wählte, deren Verbindungsschnur man momentan folgte, so ergaben sich einzelne Wörter und insgesamt der Satz: „DIESE ANZAHL RAHMEN GETEILT DURCH VIER“. Da es sich ingesamt um 12 Kästen bzw. Rahmen handelte, war die Lösung dieses Rätsel 3.
Zusammen mit der Zahl aus dem Nagelbretträtsel ergab sich somit die Rechnung: <m>12-3=9</m>
dass das Rätsel intern „Mühle-Rätsel“ hieß, da die Idee ursprünglich auf dem Spielbrett des Mühlespiels beruhte? Jemand wollte damit sein Kindheitstrauma bewältigen, dass es beim Mühlespiel keine diagonalen Verbindungen gibt.

Das Kissenrätsel
 An unserem Treffpunkt im Wald überreichte uns das URC-Team 40 Sitzkissen, um es uns etwas gemütlicher auf dem harten Waldboden einzurichten. Es gab Kissen in den vier verschiedenen Farben gelb, orange, grün und blau. Außerdem hatten alle Kissen in einer Ecke ein Symbol aufgemalt.
An unserem Treffpunkt im Wald überreichte uns das URC-Team 40 Sitzkissen, um es uns etwas gemütlicher auf dem harten Waldboden einzurichten. Es gab Kissen in den vier verschiedenen Farben gelb, orange, grün und blau. Außerdem hatten alle Kissen in einer Ecke ein Symbol aufgemalt.
dass die Symbole ursprünglich ganzflächig auf die Kissen aufmalt werden sollten? Die Macherin der Kissen wehrte sich jedoch erfolgreich gegen diese „Verunstaltung“ der armen Kissen.
Diese Symbole fanden sich auch an einer Seitenwand des Kubus wieder, sowohl als Symbole auf den schwarzen Anordnungsmustern, als auch als rote Symbole in der Mitte. Man konnte nun zunächst die Kissen mit den entsprechenden Symbolen gemäß den schwarzen Mustern auf der Kubusseite anordnen und dann wie in der Mitte durch die roten Symbole angedeutet zusammensetzen. Durch die Form der einzelnen Anordnungen ergab sich so schließlich eine vollständig gefüllte 5 Kissen breite und 8 Kissen lange Fläche.
 Entfernte man nun sämtliche gelben Kissen aus der Fläche (man erinnere sich, dass auf der anderen Kubuswand ein gelbes Kissen in Zeile 4 dargestellt war), so ergab sich die Figur der Zahl 2 aus den verbleibenen Kissen. [Das gelbe Kissen an der rechten Ecke sollte lediglich ein oranges Kissen ersetzen, was im Rätseleifer irgendwo verschollen war.]
Entfernte man nun sämtliche gelben Kissen aus der Fläche (man erinnere sich, dass auf der anderen Kubuswand ein gelbes Kissen in Zeile 4 dargestellt war), so ergab sich die Figur der Zahl 2 aus den verbleibenen Kissen. [Das gelbe Kissen an der rechten Ecke sollte lediglich ein oranges Kissen ersetzen, was im Rätseleifer irgendwo verschollen war.]
Mit der 2 hatten wir nun die letzte Ziffer für das Zahlenschloss: 4192 öffnete uns schließlich die Tür in das Innere des Kubus, wo wir einen Rechner vorfanden, der mittels eines Passwortes gesperrt war.
Das Ahnenrätsel
 Auf der hinteren Kubuswand fand sich nun noch eine große Fläche mit zahlreichen Buchstaben. Über jeder Spalte war ein Haken angebracht. Aus den Wäldern hatten wir entsprechend viele farbige Schaumstoffwürfel mitgebracht, die an verschieden langen Schnüren hingen. Es lag nahe die Schaumstoffwürfel an den Haken aufzuhängen. Eine gelbe und eine grüne Markierung auf der Leinwand gaben zwei Positionen vor. Die restlichen konnten durch Fortsetzen der Farbreihe analog zum Farbkreis an ihre entsprechende Position gebracht werden.
Auf der hinteren Kubuswand fand sich nun noch eine große Fläche mit zahlreichen Buchstaben. Über jeder Spalte war ein Haken angebracht. Aus den Wäldern hatten wir entsprechend viele farbige Schaumstoffwürfel mitgebracht, die an verschieden langen Schnüren hingen. Es lag nahe die Schaumstoffwürfel an den Haken aufzuhängen. Eine gelbe und eine grüne Markierung auf der Leinwand gaben zwei Positionen vor. Die restlichen konnten durch Fortsetzen der Farbreihe analog zum Farbkreis an ihre entsprechende Position gebracht werden.
 Die Schaumstoffwürfel fielen nun automatisch durch ihre vorgegebene Schnurlänge auf einen zugehörigen Buchstaben auf dem Buchstabenfeld. Von links nach rechts ergab sich: „LENA MARLEN LORENZ“, anscheinend ein direkte Verwandte von Hans Peter Lorenz (HaPe).
Die Schaumstoffwürfel fielen nun automatisch durch ihre vorgegebene Schnurlänge auf einen zugehörigen Buchstaben auf dem Buchstabenfeld. Von links nach rechts ergab sich: „LENA MARLEN LORENZ“, anscheinend ein direkte Verwandte von Hans Peter Lorenz (HaPe).
dass für Frau Lorenz zunächst ein anderer Vorname vorgesehen war? Ein Fehler beim Aufkleben der Buchstaben auf die Leinwand verhalf ihr zu ihrem neuen ersten Vornamen.
Ihren Namen als Passwort in den Rechner eingegeben, offenbarte uns das Abschiedsvideo von Hans Peters verstorbenen Großvater.
dass das Video im Keller der Uni gedreht wurde und das Abziehen der Klospülung in den oberen Etagen aufgrund des Rauschens in den direkt durch den Keller laufenden Abwasserrohren zum Abbruch mehrerer Aufnahmen führte?



